I include it in full, as published on Lostpedia, here:
World Line Theory in Minkowski Spacetime
We live in a four-dimensional world, with each individual occupying a specific time and space. For example, right now you are sitting right here reading your computer screen. In an hour you might be out in the yard. In two hours from now, you might be out grocery shopping. You can plot these points in a timeline from A to B to C. You’ll note that your own timeline remains constant and is measured in hours.
Conveniently on Earth, time runs at approximately the same speed so that all of our timelines are fixed. Right now you are at your computer while your friend Steve is watching the game at his house. An hour from now you are in the yard while Steve is washing his car. And two hours from now you bump into Steve at the grocery store. You can chat about your days and say how funny it is that Steve was watching the game while you were at the computer. This would be called “simultaneity” and would be fairly accurate since both timelines are fixed, even if your places in space are not.
But what if your places in time were not fixed either? For example, what if Steve went out to wash his car 45 minutes from now instead of an hour from now, but you still meet up two hours from now. However – and this is the crucial part – it still seems like an hour from now to Steve that he washes his car. His timeline of ABC is still measured in hours, just like yours, but when you compare the two timelines side-by-side, the points do not necessarily match up. This is called relativity of simultaneity.
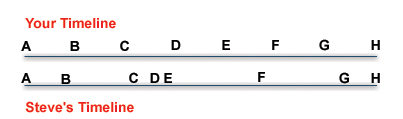
Now imagine a longer time line with points A,B,C,D,E,F,G,H. You can get some pretty funky things happening, as shown in the graph below.
From Steve’s perspective, point B on your timeline takes longer than an hour to reach, point C less than an hour from that point, and so on.
In this example, we see that both Point A and Point H align. It is not too difficult now to envision that you might actually meet up with Steve at Point G in your timeline, but somewhere between Point G and Point H in his.
One way that you would be able to measure this time difference is through the use of clocks. If you checked the time when you met at the grocery store at Point G in your timeline, your watch would say 7:00pm, whereas Steve’s watch may say 7:31pm.
Another assumption that we are working under is that distance between two points in space is constant. That is, your house is the same distance from Steve’s house at all points along the timeline, and both houses are the same distance from the grocery store at all times. However if relative distance is constantly changing as well, we move into some very mind-blowing territory – especially if you take into consideration that it still seems like the exact same distance to each person traveling it.
All of this would seem quite odd, unless you were familiar with world lines within a Minkowski spacetime. Both your timeline and that of Steve’s in this example can be considered a world line, a fairly linear line through an ever-moving time and space. This very phenomenon may be happening to us right now, but again because we are all on Earth, our world lines are the same. Time and space remain relatively (which in this case means exactly) constant.
Under this theory, I propose that in the LOST universe, the Island is somehow on a different world line. Therefore, time and space are moving along a very different trajectory.
This would explain what is happening during Daniel Faraday’s experiment. Daniel talks to Regina, setting up Point A in both their timelines. Both assume that they are still physically separated by 40 km, and that their timelines are moving at the same rate.
However since time and space are constantly moving relative to each other, this is not the case. In Regina’s timeline, the payload reaches the beacon in about 10 seconds. We know that this is not the case along Daniel’s timeline (though we don’t know exactly how much time has passed).
The explanation is that the rocket must travel between these two world lines from Point A in world line 1 to Point B in world line 2 through both time and space. During the rocket’s trip, both time and distance diverge between the freighter and the beacon. The timelines are also moving at different relative speeds. So not only does the rocket arrive at a different relative time, but also at a different point along the timeline. That explains why it takes the rocket longer to reach the beacon than it should, and why the two clocks are different.
It is important to note here too that the distance from the perspective of the rocket is still 40km, which is why it couldn’t run out of fuel (and why Daniel is not worried about the helicopter running out of fuel when he realizes what is happening). Again, distance is relative between two world lines, but needs to be constant in terms of an object traveling between two points.
A good visual representation of this phenomenon is found under the description of the Lorentz transformations in Wikipedia here: http://en.wikipedia.org/wiki/Lorentz_transformations (scroll down to the moving image on the right side).
Now although the two world lines are acting independently of each other, they may be moving roughly parallel. It is even possible that they are not acting independently at all, but that there is an algorithm that can exactly predict the coordinates of time, space and distance in one world line based on coordinates of the other world line. That is why Daniel tells Frank it is important to keep the same bearing, since following a different bearing might put him in a different time or place. As we see from the rocket, this would likely only be a matter of minutes or hours since the two world lines are so close to each other. But the possibility exists that following a different bearing could place him in a wildly different spacetime.
So where’s the literary proof in this theory? If we assume that the producers are trying to tell us something based on names, then the name Minkowski automatically points to Minkowski spacetime, a theory in physics used to explain Einstein’s theory of special relativity. This uses Lorentz transformations to predict that time is relative (called time dilation). From this we get the concept of world lines, which plots time and space along a linear line in Minkowski spacetime. But, due to special relativity, two world lines may have much different paths. Therefore, we can never assume that a point on one world line is the same as a point on another world line the (Relativity_of_simultaneity).
A similar idea describing the different passages of time (and obviously place) is also put forward in C.S. Lewis’s Narnia series – and now we have a character named Charlotte Staples Lewis.
Interestingly, Lorentz transformations are also used in electromagnetic theory, which is described using Maxwell’s equations (note the introduction of the Maxwell Group in the most recent ARG). In turn, this is connected to the work of Michael Faraday.
Finally, the producers have basically stated that time does not work the same way on the Island, so obviously there is something going on. This theory explains Daniel’s experiment and holds true to everything we know so far.